Introduction to Tamarin

Tamarin is a security protocol verification tool used to identify attacks from adversaries that can leak information during the execution of said protocol. Tamarin uses symbolic reasoning and multiset term rewriting to automatically construct proofs that show a protocol is safe against adversaries for an arbitrary amount of instances of said protocol.

Tamarin has a full guide and manual available on their website , which is good introduction to the tool and extensive behavior. This page serves as additional information that would have helped me when I first began utilizing the tool as well, and is meant only to be supplemental to the offical manual.

First Example

This tutorial will use the same example that the official manual uses. However, this example will go a lot slower, and, in general, include more details for the less cryptographically minded. If you are already familiar with inference rules and multiset term rewriting, using the official manual or skipping this section is suggested.

A full copy of the protocol written in the section can be found here, ready to run.

Starting the model

First, let's set up the file outline. We begin by naming the theory we are going to describe in a file named TamarinExample.spthy. Tamarin comments use // or /* */, so I use those to show where the protocol itself is written.

						
		theory FirstExample begin
			/* */
		end

This is the theory we will write:

$\begin{matrix} C \to S : & {k}_{p k s} \\ S \to C : & h (k) \end{matrix}$

First, $C$ sends $S$ an encrypted value, $k$ (encrypted with key $pks$ ). $S$ then returns the hash of the value to confirm $k$ was correctly received. To begin writing this theory, we first need to write a system to create encryption keys, use them, and reveal them.

Key Registration

Let's begin with the registration of a new key.

						
		theory FirstExample begin
	+		builtins: hashing, asymmetric-encryption
			
	+		rule Register_pk:
	+			[ Fr(~ltk) ]
	+		-->
	+			[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
		end

What do these changes do?

Since we know we'll use both hashing, and asymmetric encryption; since Tamarin has built in libraries for both of these, we include them under the builtins section.
We define a new rule that lets us write a new inference rule about the system.
The [ LHS ] --> [ RHS ] is the inference rule itself. The LHS is the assumption we are making about the system, and if satisify the assumption, we can draw the conclusions in RHS.
Fr(~ltk) assumes the generation of a new variable, ~ltk, which is unused in previous rules. Generating fresh variables can be done anytime, and are abstracted away from concrete values. This means they can represent keys or secrets in a protocol.
!Ltk($A, ~ltk) is a fact in Tamarin. Fact names are determined by the model writer, and represent accessible peices of knowledge that protocol parties or adversaries can obtain. In this case, we name the fact !Ltk to represent a long-term private key for the protocol's execution and we associate it with the owner, $A.
In Tamarin, the ! represents persistance - !Ltk can be assumed again and again, without any changes. If the ! were not present, a new key would be generated everytime the model referenced this fact.
The $ in $A indicates publicity. A is a public value, which can be accessed and seen by any party, adversary or not.
The fact !Pk($A, pk(~ltk)) associates $A with the public value of ~ltk. The pk( KEY ) is a function defined in the asymmetric encryption library, and represents the public key for other parties to use.
So, in summary, this rule generates a new key, and uses two facts to associate the private key and it's public counterpart with the owner of the key.

Let's look at the next section of the key creation, publishing the public version for others to use and with which others encrypt messages.

						
		theory FirstExample begin
			builtins: hashing, asymmetric-encryption
			
			rule Register_pk:
				[ Fr(~ltk) ]
			-->
				[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
			
	+		rule Get_pk:
	+			[ !Pk(Owner, pubkey) ]
	+		-->
	+			[ Out(pubkey) ]
		end

What about these changes? What do they do?

Here, we assume !Pk(Owner, pubkey) - we are given the public key fact that associates some Owner with some pubkey.
Given this fact, we output pubkey. The Out fact is a Tamarin-reserved fact that publishes the given value on an unsecured network, where adversaries and parties can access the given value.
Out(value)'s corresponding fact is In(value), which any fact can assume, and is listening on the unsecured network for published messages.
Additionally, note that in rule Register_pk, we use ~ltk and $A, and Get_pk does not use ~ or $. In Tamarin, special characters are considered to be part of the variable, so in Register_pk, ltk is different from ~ltk.

Let's add the last part of the key - revealing it to everybody after it's not being used anymore.

						
		theory FirstExample begin
			builtins: hashing, asymmetric-encryption
			
			rule Register_pk:
				[ Fr(~ltk) ]
			-->
				[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
			
			rule Get_pk:
				[ !Pk(Owner, pubkey) ]
			-->
				[ Out(pubkey) ]
			
	+		rule Reveal_Ltk:
	+			[ !Ltk(A, ltk) ]
	+		--[ LtkReveal(A) ]->
	+			[ Out(ltk) ]
		end

How do these changes work?

Given the long-term key, this rule publishes the private key, very similar to the rule Get_pk.
One noticable difference is the inference arrow. Instead of -->, we use --[ LtkReveal(A) ]->. This is an Action Fact. Action facts annotate the traces construted by the inference rules, and allow for reasoning over traces in the protocol. This action fact has no impact on the rule, but lets us see in a trace that the key has been revealed.

First Lemma

Lemmas in Tamarin describe desired behavior of the model, which can then be proven or counter-examples identified. This is where the action facts start to be utilized. For details on how the proofs in Tamarin actually work, see the official tamarin manual. Right now, we are going to write a toy, sanity lemma for us to visualize how Tamarin works.

						
		theory FirstExample begin
			builtins: hashing, asymmetric-encryption
		
			rule Register_pk:
				[ Fr(~ltk) ]
			-->
				[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
			
			rule Get_pk:
					[ !Pk(Owner, pubkey) ]
			-->
				[ Out(pubkey) ]
			
			rule Reveal_Ltk:
				[ !Ltk(A, ltk) ]
			--[ LtkReveal(A) ]->
				[ Out(ltk) ]
			
	+		lemma Sanity_Reveal_Occurs:
	+			exists-trace
	+			"Ex Cli #t. LtkReveal(Cli)@t"
		end

How does this lemma work?

The exists-trace indicates that the lemma should search for at least one instance that satisfies the following property. Otherwise, all-traces can be used, which checks that every possible trace satisfies the property. If neither are specified, all-traces is defaulted to.
In English, the property in quotes states "There exists a client and timestamp t such that LtkReveal(client) occurs at time t". Because Tamarin does not have a type system, it is up to the modeler to keep track of the types in facts and lemmas.
The # specifies that t is a timestamp, and when used, must be proceeded by a # or @.
Using the interactive Tamarin prover, we can automatically prove this lemma very easily. If Tamarin is installed correctly, we can run "tamarin-prover interactive <directory/file>" and navigate on a web browser to "localhost:3001". We then select the theory, and can see the different options to begin the proof.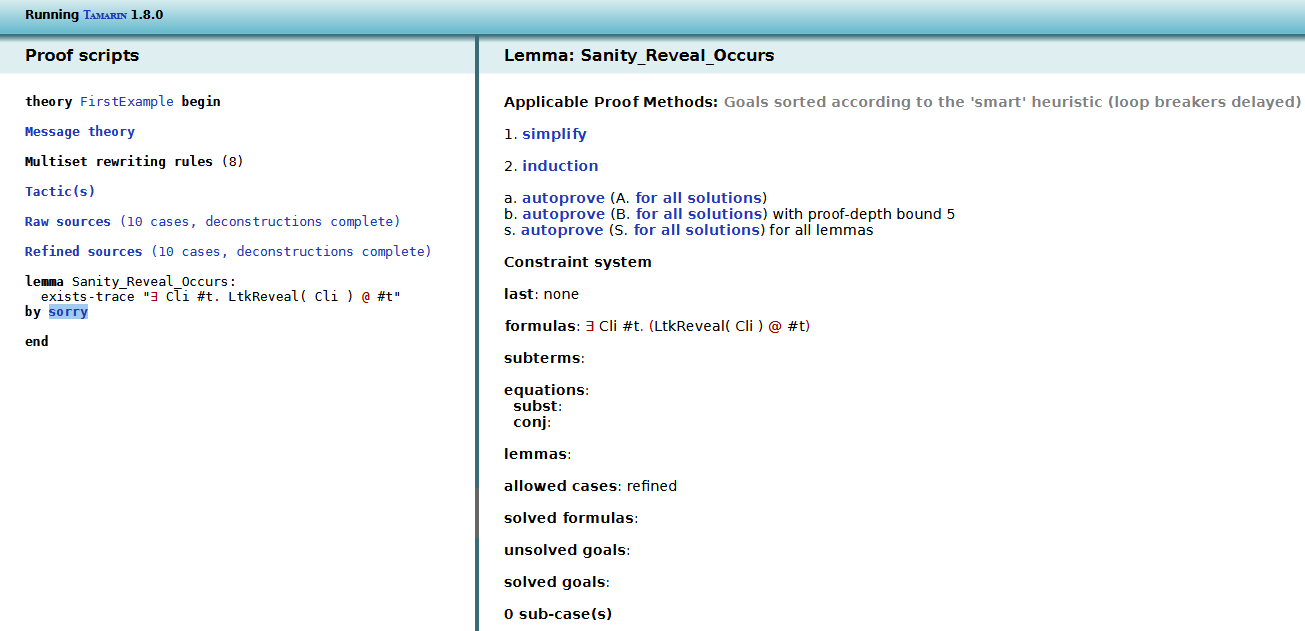
Here, we can press "a" and use the default heuristic to prove the lemma. The trace Tamarin finds is shown here:

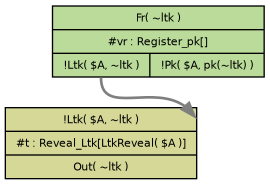
As a brief overview of how the prover works, Tamarin starts with the possible cases for the LtkReveal, and works backwards to find sources that satisfy the trace. Here, we can see that Tamarin starts with the inference rule with LtkReveal(A) and searches for a source for !Ltk($A, ~ltk). Since it finds Register_pk as the source, it attempts to find sources for Register_pk. However, since Register_pk only requires a fresh nonce, and those do not need sources, it has completed it's search, and returns the successful trace.

Client Protocol

Let's move on to modeling the client interaction portion of the protocol, starting with the first message: $\begin{matrix} C \to S : & {k}_{p k s} \end{matrix}$

						
		theory FirstExample begin
			builtins: hashing, asymmetric-encryption
			
			rule Register_pk:
				[ Fr(~ltk) ]
			-->
				[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
			
			rule Get_pk:
				[ !Pk(Owner, pubkey) ]
			-->
				[ Out(pubkey) ]
			
			rule Reveal_Ltk:
				[ !Ltk(A, ltk) ]
			--[ LtkReveal(A) ]->
				[ Out(ltk) ]
			
	+		rule C_Step_1:
	+			[ Fr(~k)
	+			, !Pk($S, pks)
	+			]
	+		-->
	+			[ Client_1($S, ~k)
	+			, Out(aenc(~k, pks) )
	+			]
			
			lemma Sanity_Reveal_Occurs:
				exists-trace
				"Ex Cli #t. LtkReveal(Cli)@t"
		end

Here, the client generates the secret they wish to send to the server, and obtains server's private key, using techniques from earlier.
The client uses Out(aenc(~k, pks)) to encrypt the message (using a fucntion from asymmetric-encryption), and output on the network.
Lastly, we have the fact Client_1($S, ~k). This fact let's us "save" the information for another inference rule. Since there is no !, it can only be consumed once.

Let's add the second message of the protocol: $\begin{matrix} S \to C : & h (k) \end{matrix}$

						
		theory FirstExample begin
			builtins: hashing, asymmetric-encryption
			
			rule Register_pk:
				[ Fr(~ltk) ]
			-->
				[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
			
			rule Get_pk:
				[ !Pk(Owner, pubkey) ]
			-->
				[ Out(pubkey) ]
			
			rule Reveal_Ltk:
				[ !Ltk(A, ltk) ]
			--[ LtkReveal(A) ]->
				[ Out(ltk) ]
			
			rule C_Step_1:
				[ Fr(~k)
				, !Pk($S, pks)
				]
			-->
				[ Client_1($S, ~k)
				, Out(aenc(~k, pks) )
				]
			
	+		rule C_Step_2:
	+			[ Client_1(S, k)
	+			, In( h(k) )
	+			]
	+		--[ SessKeyC(S, k) ]->
	+			[]
			
			lemma Sanity_Reveal_Occurs:
				exists-trace
				"Ex Cli #t. LtkReveal(Cli)@t"
		end

We reuse the fact we stored earlier as Client_1($S, ~k). When this inference rule is used during a proof, only one occurance of the Client_1 fact can happen in a trace, because it is not persistant.
We also intake the hash of the same key we generated earlier using In(h(k)).
After this, the client's role in the protocol is done, so we draw no conclusion on the right hand side.
Lastly, we annotate this with the action fact SessKeyC(S,k) so we can reason over the client sending the message in future lemmas.

To finish this model off, we just need to model the server that handles incoming requests and outputs the hash.

						
		theory FirstExample begin
			builtins: hashing, asymmetric-encryption
			
			rule Register_pk:
				[ Fr(~ltk) ]
			-->
				[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
			
			rule Get_pk:
				[ !Pk(Owner, pubkey) ]
			-->
				[ Out(pubkey) ]
			
			rule Reveal_Ltk:
				[ !Ltk(A, ltk) ]
			--[ LtkReveal(A) ]->
				[ Out(ltk) ]
			
			rule C_Step_1:
				[ Fr(~k)
				, !Pk($S, pks)
				]
			-->
				[ Client_1($S, ~k)
				, Out(aenc(~k, pks) )
				]
			
			rule C_Step_2:
				[ Client_1(S, k)
				, In( h(k) )
				]
			--[ SessKeyC(S, k) ]->
				[]
			
	+		rule S_Step_1:
	+			[ !Ltk($S, ~ltkS)
	+			, In( request )
	+			]
	+		--[ AnswerRequest($S, adec(request, ~ltkS)) ]->
	+			[ Out( h(adec(request, ~ltkS)) ) ]
			
			lemma Sanity_Reveal_Occurs:
				exists-trace
				"Ex Cli #t. LtkReveal(Cli)@t"
		end

The server uses it's own long-term key by infering !Ltk($S, ~ltkS), and recieves an encrypted request from the network with In(request).
The server then outputs the hash of the decrypted message using Out( h(adec(request, ~ltkS)) ). Because the input was encrypted, this works only if the key that encrypted the message corresponds to the private decryption key. Tamarin's library for asymmetric-encryption uses function and equations to make sure these values on comparable. (See section on functions).
The action fact AnswerRequest($S, adec(request, ~ltkS)) annotates that the server is responding to request.

Security Properties

Let's take a look at some of the security properties for the protocol. In brief, we want to write properties for:

If a client is using a key 'k', then the adversary only knows 'k' if it has been revealed.
For all keys 'k' used by clients, a server answered the request or there was a reveal before the key was set up.
It is possible for a session to hold without a reveal occuring on the key.

Let's go over each of these step-by-step. Note: when the formal FOL is written, timestamps are ignored to avoid use of temporal logic, which would likely be confusing to include here.

If a client is using a key 'k', then the adversary only knows 'k' if it has been revealed.
- If we state this in more structured english, we can say: "In all traces, it is not the case that there is a server and secret such that the adversary knows the secret and a long term reveal has not occurred."
- Writing this formally, we can use the action facts to say: $\neg (\exists S e r v, s e c | S e s s K e y C (S e r v, \sec) \land K (\sec) \land \neg (L t k R e v e a l (S e r v)))$ The $K(sec)$ in the formula is how we denote the adversary's knowledge.
- When we convert this formula to Tamarin, we will write almost the same lemma, but we must also include time stamps on all action facts. In the end, the Tamarin code will look like this: (Note: some of the previous code has been compressed for readability)
```
									
	theory FirstExample begin
		builtins: hashing, asymmetric-encryption
		
		rule Register_pk:
			[ Fr(~ltk) ] --> [ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
		
		rule Get_pk:
			[ !Pk(Owner, pubkey) ] --> [ Out(pubkey) ]
		
		rule Reveal_Ltk:
				[ !Ltk(A, ltk) ] --[ LtkReveal(A) ]-> [ Out(ltk) ]
		
		rule C_Step_1:
			[ Fr(~k), !Pk($S, pks)] --> [ Client_1($S, ~k), Out(aenc(~k, pks) )]
		
		rule C_Step_2:
			[ Client_1(S, k), In( h(k) )] --[ SessKeyC(S, k) ]-> []
		
		rule S_Step_1:
			[ !Ltk($S, ~ltkS), In( request )] --[ AnswerRequest($S, adec(request, ~ltkS)) ]-> [ Out( h(adec(request, ~ltkS)) ) ]
		
		lemma Sanity_Reveal_Occurs: exists-trace "Ex Cli #t. LtkReveal(Cli)@t"
		
+		lemma Client_session_key_secrecy:
+			all-traces
+			"not ( Ex Serv key #i #j.
+				SessKeyC(Serv, key)@i
+				& K(key)@j
+				& not( Ex #r. LtkReveal(Serv)@r )
+			)"
	end
									
								
```
- Most of the formal sentence translates directly to Tamarin, such as $\exists$ directly to Ex. If timestamps are ignored, it is easy to write the lemmas as FOL, and then translate them into Tamarin, before adding timestamps and time restrictions back in.
- It is important to note that all Tamarin lemmas must be written in guarded FOL. (See section Lemmas for additional information.)

For all keys 'k' used by clients, a server answered the request or there was a reveal before the key was set up.

In structured english, we can say: "For all servers and secrets, if they were set up, then there is either a server that answered the request, or the adversary performed a reveal before the setup occured."
Formally, we can state: $\forall S e r v, s e c | S e s s K e y C (S e r v, \sec) ⟹ (A n s w e r R e q u e s t (S e r v, k e y) \lor L t k R e v e a l (S e r v))$
In Tamarin, this translates to

									
	theory FirstExample begin
		builtins: hashing, asymmetric-encryption
		
		rule Register_pk:
			[ Fr(~ltk) ] --> [ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
		
		rule Get_pk:
			[ !Pk(Owner, pubkey) ] --> [ Out(pubkey) ]
		
		rule Reveal_Ltk:
				[ !Ltk(A, ltk) ] --[ LtkReveal(A) ]-> [ Out(ltk) ]
		
		rule C_Step_1:
			[ Fr(~k), !Pk($S, pks)] --> [ Client_1($S, ~k), Out(aenc(~k, pks) )]
		
		rule C_Step_2:
			[ Client_1(S, k), In( h(k) )] --[ SessKeyC(S, k) ]-> []
		
		rule S_Step_1:
			[ !Ltk($S, ~ltkS), In( request )] --[ AnswerRequest($S, adec(request, ~ltkS)) ]-> [ Out( h(adec(request, ~ltkS)) ) ]
		
		lemma Sanity_Reveal_Occurs: exists-trace "Ex Cli #t. LtkReveal(Cli)@t"
		
		lemma Client_session_key_secrecy:
			all-traces
			"not ( Ex Serv key #i #j.
				SessKeyC(Serv, key)@i
				& K(key)@j
				& not( Ex #r. LtkReveal(Serv)@r )
			)"
			
+		lemma Client_Auth:
+			all-traces
+			"All Serv sec #i. SessKeyC(Serv, sec)@i
+			==> (
+				(Ex #a. AnswerRequest(Serv, sec)@a)
+				|
+				(Ex #r. LtkReveal(Serv)@r & #r<#i)
+			)"
	end

Since we ignored the timestamps when writing the FOL, note that we had to add them back by stating the LtkReveal occurs before the session is initiated with #r<#i.

It is possible for a session to hold without a reveal occuring on the key.

In structured English, we can write that "there exists a trace where there exists a session and secret that has been initiated and there does not exist a reveal.
Formally, this becomes: $\exists S e r v, s e c | (S e s s K e y C (S e r v, s e c) \land \neg (L t k R e v e a l (s e r v))$
Inputting into tamarin gives us:

									
	theory FirstExample begin
		builtins: hashing, asymmetric-encryption
		
		rule Register_pk:
			[ Fr(~ltk) ] --> [ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
		
		rule Get_pk:
			[ !Pk(Owner, pubkey) ] --> [ Out(pubkey) ]
		
		rule Reveal_Ltk:
				[ !Ltk(A, ltk) ] --[ LtkReveal(A) ]-> [ Out(ltk) ]
		
		rule C_Step_1:
			[ Fr(~k), !Pk($S, pks)] --> [ Client_1($S, ~k), Out(aenc(~k, pks) )]
		
		rule C_Step_2:
			[ Client_1(S, k), In( h(k) )] --[ SessKeyC(S, k) ]-> []
		
		rule S_Step_1:
			[ !Ltk($S, ~ltkS), In( request )] --[ AnswerRequest($S, adec(request, ~ltkS)) ]-> [ Out( h(adec(request, ~ltkS)) ) ]
		
		lemma Sanity_Reveal_Occurs: exists-trace "Ex Cli #t. LtkReveal(Cli)@t"
		
		lemma Client_session_key_secrecy:
			all-traces
			"not ( Ex Serv key #i #j.
				SessKeyC(Serv, key)@i
				& K(key)@j
				& not( Ex #r. LtkReveal(Serv)@r )
			)"
			
		lemma Client_Auth:
			all-traces
			"All Serv sec #i. SessKeyC(Serv, sec)@i
			==> (
				(Ex #a. AnswerRequest(Serv, sec)@a)
				|
				(Ex #r. LtkReveal(Serv)@r & #r<#i)
			)"
			
+		lemma Sanity_Session_Occurs:
+			exists-trace
+			"Ex Serv sec #i. (
+				SessKeyC(Serv, sec)@i
+				& not( Ex #r. LtkReveal(Serv)@r )
+			)"
	end

After completing these lemmas, let's take a closer look at the results after we automatically prove all of the lemmas in our file. This is the result for the last lemma, Sanity_Session_Occurs:

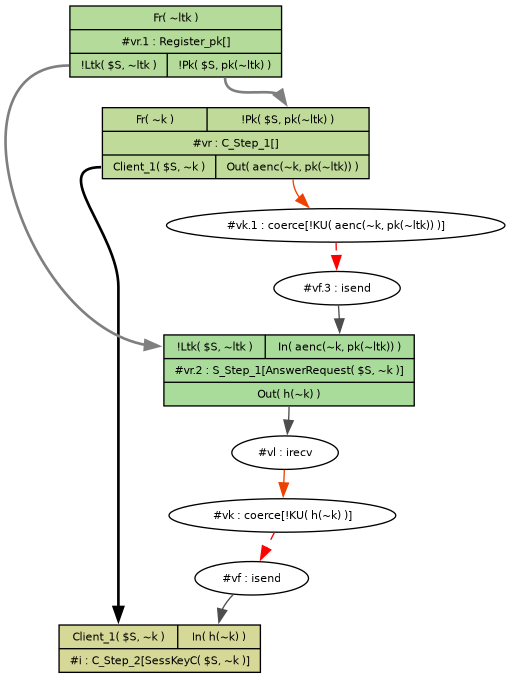
We can see that for each inference rule, every fact on the left hand side has been sourced back to fresh values. Additionally, Tamarin uses circular nodes to show adversary intervention, and is automatically enabled during verification. For more information on the adversary, see section Adversaries.

Success!

If you got to this point, that means you have successfully run the Tamarin first example. Congratulations! You are now ready to begin proving the security of your own protocols.

The Tamarin Language

Language guide to come.

Lemmas

Lemma guide to come.

Functions

Function guide to come.

Oracles

Oracle guide to come.

Macros

Macro guide to come.